Heawood graph
| Heawood graph | |
|---|---|
| Named after | Percy John Heawood |
| Vertices | 14 |
| Edges | 21 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 6 |
| Automorphisms | 336 (PGL2(7)) |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Properties | Bipartite Cubic Cage Distance-transitive Distance-regular Toroidal Hamiltonian Symmetric |
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.[1]
Contents |
Combinatorial properties
The graph is cubic, and all cycles in the graph have six or more edges. Every smaller cubic graph has shorter cycles, so this graph is the 6-cage, the smallest cubic graph of girth 6. It is a distance-regular graph.[2]
There are 24 perfect matchings in the Heawood graph; for each matching, the set of edges not in the matching forms a Hamiltonian cycle. For instance, the figure shows the vertices of the graph placed on a cycle, with the internal diagonals of the cycle forming a matching. By subdividing the cycle edges into two matchings, we can partition the Heawood graph into three perfect matchings (that is, 3-color its edges) in eight different ways (Brouwer). Every two perfect matchings, and every two Hamiltonian cycles, can be transformed into each other by a symmetry of the graph.[3]
Geometric and topological properties
The Heawood graph is a toroidal graph; that is, it can be embedded without crossings onto a torus. One embedding of this type places its vertices and edges into three-dimensional Euclidean space as the set of vertices and edges of a nonconvex polyhedron with the topology of a torus, the Szilassi polyhedron.
The graph is named after Percy John Heawood, who in 1890 proved that in every subdivision of the torus into polygons, the polygonal regions can be colored by at most seven colors.[4][5] The Heawood graph forms a subdivision of the torus with seven mutually adjacent regions, showing that this bound is tight.
The Heawood graph is also the Levi graph of the Fano plane, the graph representing incidences between points and lines in that geometry. It has crossing number 3, and is the smallest cubic graph with that crossing number (sequence A110507 in OEIS). Including the Heawood graph, there are 8 distinct graphs of order 14 with crossing number 3.
The Heawood graph is a unit distance graph: it can be embedded in the plane such that adjacent vertices are exactly at distance one apart, with no two vertices embedded to the same point and no vertex embedded into a point within an edge. However, the known embeddings of this type lack any of the symmetries that are inherent in the graph.[6]
Algebraic properties
The automorphism group of the Heawood graph is isomorphic to the projective linear group PGL2(7), a group of order 336.[7] It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Heawood graph is a symmetric graph. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Heawood graph, referenced as F014A, is the only cubic symmetric graph on 14 vertices.[8][9]
The characteristic polynomial of the Heawood graph is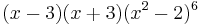 
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
Gallery
References
- ^ Weisstein, Eric W., "Heawood Graph" from MathWorld.
- ^ Brouwer, Andries E.. "Heawood graph". Additions and Corrections to the book Distance-Regular Graphs (Brouwer, Cohen, Neumaier; Springer; 1989). http://www.win.tue.nl/~aeb/drg/graphs/Heawood.html.
- ^ Abreu, M.; Aldred, R. E. L.; Funk, M.; Jackson, Bill; Labbate, D.; Sheehan, J. (2004), "Graphs and digraphs with all 2-factors isomorphic", Journal of Combinatorial Theory, Series B 92 (2): 395–404, doi:10.1016/j.jctb.2004.09.004, MR2099150.
- ^ Brown, Ezra (2002). "The many names of (7,3,1)". Mathematics Magazine 75 (2): 83–94. doi:10.2307/3219140. JSTOR 3219140. http://www.math.vt.edu/people/brown/doc/731.pdf.
- ^ Heawood, P. J. (1890). "Map colouring theorems". Quarterly J. Math. Oxford Ser. 24: 322–339.
- ^ Gerbracht, Eberhard H.-A. (2009). Eleven unit distance embeddings of the Heawood graph. arXiv:0912.5395..
- ^ Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. New York: North Holland. p. 237. ISBN 0-444-19451-7. http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html.
- ^ Royle, G. "Cubic Symmetric Graphs (The Foster Census)."
- ^ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002.